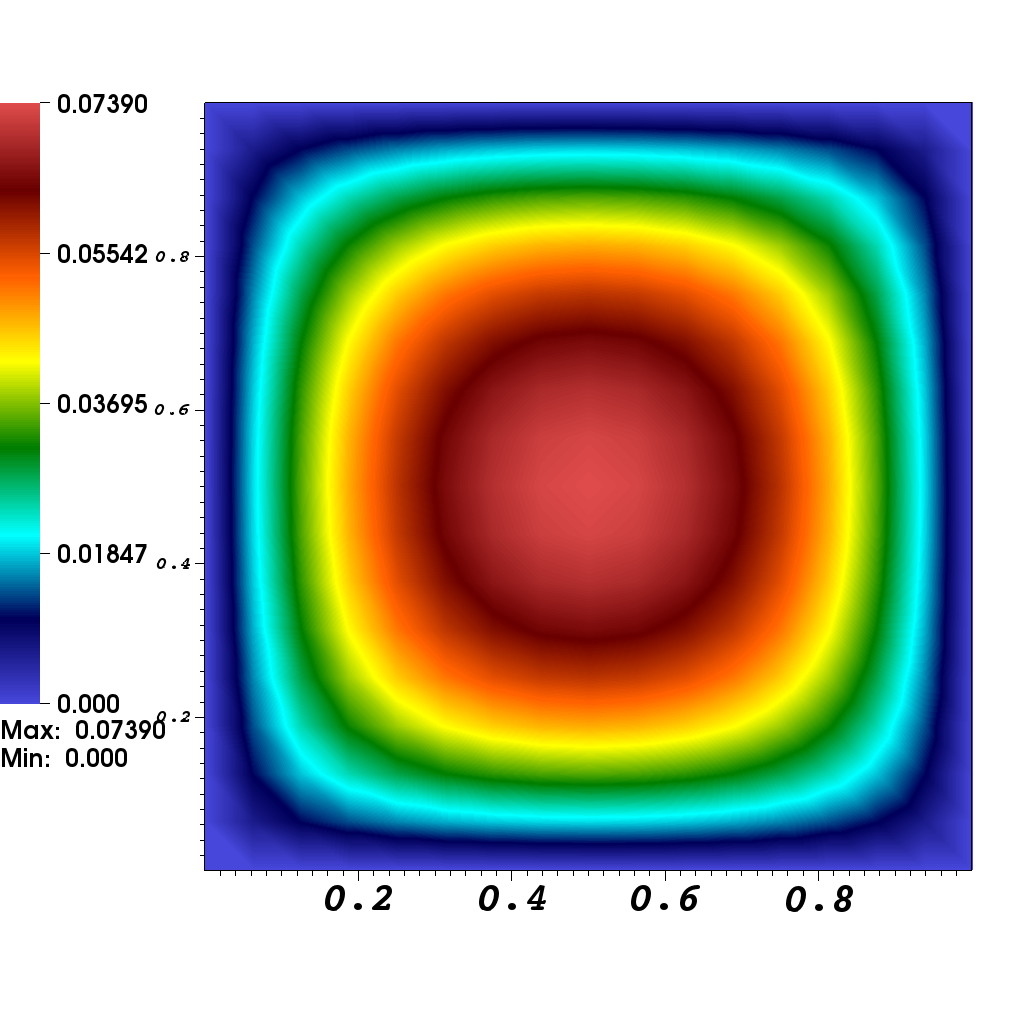
Cálculo numérico de ecuaciones diferenciales parciales
Clase abierto internacional: IntNumPDE
Número del curso en LUH: 10116
Semestre de invierno 2020/2021 en la universidad de Leibniz en Hanover
♦Apoyo financiero y administrativo:
- PeCCC - Peruvian Competence Center of Scientific Computing
- DAAD (German Academic Exchange Service)Leibniz University Hannover International Office
♦Novedades:
Apr 10, 2021:Video on the Lax-Milgram lemmaJan 26, 2021: Meeting 14 (Questions and Quiz)
Dec 22, 2020:Video explaining Galerkin orthogonality and Cea's lemma
Dec 15, 2020:Video meeting 10
Dec 08, 2020:Video meeting 9a
Dec 08, 2020:Video meeting 9b
Nov 22, 2020:Enlace a un sitio con más informaciones para tarea 6 (semana Nov 23-27)
Nov 17, 2020:Vídeo explicando el método de elementos finitos
Nov 14, 2020:Vìdeo: Los prrimeros 20 minutos de clase 2 (Oct 20, 2020)
Nov 14, 2020:Vìdeo: Resumen de la primera clase (Oct 13, 2020)
Nov 11, 2020:Vídeo explicando EDPs y sus clasificaciones
Oct 27, 2020:Vídeo explicando el método de diferencias finitas
Oct 27, 2020: Actualización de notas de clase: (Capítulo 17: Poisson 2D en python)
Oct 14, 2020: Actualización de notas de clase: Capítulo 17 Software (NUEVO), ampliado unos partes del capítulo 2 acabas de la última clase, corregido unos errores en capítulo 3.8
Sep 29, 2020: Actualización (capítulo 2) de notas de clase
Sep 12, 2020: El resumen escrito a mano (inglés)
♦Notas editadas de clase
Jan 26, 2021: Meeting 14 (Questions and Quiz)Jan 19, 2021: Edited lecture notes L21 to L26 (Chapter 10 and 12)
Jan 12, 2021: Notas editadas L21 a L24 (Chapter 10 and 12)
Jan 05, 2021: Notas editadas L21 a L22
Dec 01, 2020: Notas editadas L1 a L16
Nov 24, 2020: Notas editadas L1 a L14
Nov 17, 2020: Notas editadas L1 a L12
Nov 10, 2020: Notas editadas L1 a L10
Nov 03, 2020: Notas escritas a mano, clase 4
Nov 03, 2020: Notas editadas L1 a L8
Oct 27, 2020: Notas editadas L1 a L6
Oct 20, 2020: Notas escritas a mano, clase 2
Oct 20, 2020: Notas editadas L1 a L4
Oct 13, 2020: Notas escritas a mano, clase 1
Oct 13, 2020: Notas editadas L1/2
♦Hojas de tareas:
- Tareas para participantes de Peru tienen lugar el martes/miércoles 16h15-17h45 CET (9h15-10h45 tiempo peruano), comenzando Oct20/Oct21.
Jan 12, 2021: Hoja de tareas 11 (en español)
Jan 05, 2021: Hoja de tareas 10 (en español)
Dec 15, 2020: Hoja de tareas 9 (en español)
Dec 08, 2020: Hoja de tareas 8 (en español)
Dec 01, 2020: Hoja de tareas 7 (en español)
Nov 24, 2020: Hoja de tareas 6 (en español)
Nov 17, 2020: Hoja de tareas 5 (en español)
Nov 10, 2020: Hoja de tareas 4 (en español)
Nov 03, 2020: Hoja de tareas 3 (en español)
Oct 27, 2020: Hoja de tareas 2 (en español)
Oct 13, 2020: Hoja de tareas 1 (en español))
♦Registro para participantes de Peru
Registro♦Resumen:
Este curso se dedica a la solución numérica de las ecuaciones diferenciales parciales (EDP). Una EDP es una función de (por lo menos) dos variables independientes en la cual puede aparecer información tanto de sus derivadas como de sus valores. Las EDPs son de gran importancia en las áreas de mecánica de medios continuos para las aplicaciones de modelación en física, biología, química, finanzas, ingeniería mecánica/civil/ambiental. El curso se centra en la modelación numérica de EDPs, la cual nos permite discretizarlas para simulaciones de computador. Discutiremos diferentes esquemas de discretización, el diseño de algoritmos y su análisis numérico riguroso. Además, discutiremos la solución numérica de los sistemas de ecuaciones lineales generadas. Este curso es una parte importante de computación científica educativa en la cual la modelación matemática, métodos numéricos e implementaciones de computador interactúan.♦Audiencia / Conocimientos previos:
Los conocimientos previos son clases de cálculo, álgebra lineal y una introducción al cálculo numérico. Clases sobre la teoría de ecuaciones diferenciales ordinarias (EDO) son útiles, pero no obligatorias. Además, clases de mecánica de medios continuos pueden ser útiles, pero tampoco son obligatorias.♦Periodo (semestre de invierno en Alemania):
12 de octubre de 2020 - 29 de enero 2021♦Formato:
- autoestudio con la ayuda de materiales de estudios proporcionados (cada semana se distribuirá material de estudio para 2x90 minutos)
- combinación de elementos y discusiones en vivo (aproximadamente cada dos semanas, el martes o miércoles, 90 minutos)
- cada semana ejercicios en vivo (90 minutos)
- será anunciado: la herramienta en línea para los elementos y discusiones en vivo va a ser anunciado al comienzo de septiembre 2020
♦Volumen de trabajo:
- 10 ECTS (European Credit Transfer and Accumulation System)
- material escrito y conferencias en vivo: 180 minutos por semana
- cada semana ejercicios en vivo
- preparar soluciones para ejercicios individualmente
- consolidación del contenido mediante el autoestudio o trabajo en grupo local
- número de clases: 26-28 clases durante el semestre
- número de ejercicios: 13-14
♦Contenido:
- L1: recapitulación de conceptos característicos de la matemática numérica
- L2-L3: repaso breve de modelación matemática de ecuaciones diferenciales
- L4: clasificaciones
- L5-L8: método de diferencias finitas (FD) para problemas elípticos con condiciones de borde
- L9-L20: método de elementos finitos (FEM) para problemas elípticos de condiciones de borde
- L21-L23: solución numérica de problemas discretizados
- L24-L26/27: métodos para problemas parabólicos e hiperbólicos (EDPs dependientes del tiempo)
- L28: recapitulación del contenido
- Si el tiempo lo permite: métodos numéricos para problemas no lineales y acoplados
♦Literatura:
| 1) | T. Wick;
Numerical Methods for Partial Differential Equations Hannover : Institutionelles Repositorium der Leibniz Universität Hannover, 369 pages, 2020. DOI: https://doi.org/10.15488/9248 | Link | ||||
| 2) | Más literatura (clásica/famosa y más reciente) se puede encontrar en el capítulo 1 de la referencia 1) | |||||
| 3) | P. Bastian, T. Wick;
PeC3 Spring School on Introduction to Numerical Modeling with Differential Equations Hannover : Institutionelles Repositorium der Leibniz Universität Hannover, 2019. DOI: https://doi.org/10.15488/6427 DOI: Pre-course DOI: Exercises PeCCC - Peruvian Competence Center of Scientific Computing | Link | ||||
| 4) |
Basics in numerical mathematics: A. Quarteroni, R. Sacco, F. Saleri; Numerical Mathematics Springer, 2nd edition, 2007 DOI: 10.1007/b98885 | Link |
♦ Examen/Evaluación para estudiantes locales de Hanover:
mediados/finales de febrero 2021♦ Asistentes del profesor:
Jan Philipp Thiele, Julian Roth, Max Schröder, Gina Kleinsteinberg♦Contacto:
Diseño de freecsstemplates